Hvad er energi?
Begrebet energi er grundlæggende knyttet til bevægelse: En genstand der bevæger sig, har energi i kraft af sin bevægelse, og ved at overføre energien helt eller delvist til sine omgivelser kan den sætte disse i bevægelse eller udføre et arbejde på dem. De kræver altså energi at få en motor til at dreje rundt, at få en højttaler til at sætte luften i svingninger som lydbølger eller at sætte elektronerne i en fladskærm i bevægelse, så de udsender lys.
Men energi er mere end blot bevægelse. Der findes mange forskellige former for energi, og bevægelsesenergi (eller kinetisk energi som man kalder den) er kun én blandt disse energiformer. Alle energiformerne kan imidlertid omsættes til hinanden, og som i eksemplerne ovenfor viser, er det ofte den kinetiske energi man i sidste ende udnytter.
Historisk set tog energibegrebet også sin begyndelse med kinetisk energi eller, som man kaldte det, den vis viva ('levende kraft') der er tilknyttet legemers bevægelse. En genstand der støder ind i en anden genstand, kan sætte denne i bevægelse, og jo hurtigere den første genstand bevæger sig, jo større evne har den til at sætte andre ting i bevægelse. Det er denne evne der får et kvantitativt udtryk gennem den kinetiske energi. Nedenfor vil vi give en række eksempler på forskellige energiformer og hvordan de kan omsættes til hinanden.
Hvis man synes det til tider kan virke lidt abstrakt, er man ikke alene. Den amerikanske fysiker og nobelprismodtager Richard Feynman har udtrykt det på denne måde: "Det er vigtigt at forstå at i nutidens fysik har vi ikke nogen viden om hvad energi er […] Den er en abstrakt ting i den forstand at den ikke fortæller os noget om mekanismen eller årsagerne bag de forskellige formler".
Energiens store betydning som fysisk begreb skyldes især at den er bevaret. Det vil sige at når et system udveklser energi med sine omgivelser, ændrer den samlede energi (dvs. systemets energi plus omgivelsernes energi) sig ikke, uanset hvor kompliceret systemet eller de processer der forløber i det, er. Et system kan udveksle energi med sine omgivelser på to måder: ved at udføre et arbejde på dem eller ved at udveksle varme med dem. Når man holder regnskab med energien, viser det sig altid at systemet mister lige så meget energi som omgivelserne vinder, dvs. at den samlede energi er konstant.
Når man hverken kan skabe energi eller få den til at forsvinde, kan man undre sig over at man taler om at forbruge energi og vigtigheden af at spare på energien. Det skyldes imidlertid at ikke alle energiformer er lige nyttige. Den betragtelige mængde varmeenergi (indre energi) der findes i en liter vand ved 20 °C, kan ikke udnyttes til at udføre et nyttigt arbejde. Varmeenergi kan kun udnyttes hvis temperaturen er væsentlig højere end omgivelsernes, og den kan aldrig udnyttes fuldt ud (se også energikonvertering og varme).
Det kan derimod kemisk eller elektrisk energi som derfor er mere værdifulde energiformer i praksis. Når man taler om effektivitet af en vis proces, fx omsætningen af elektricitet til bevægelse i en elektrisk motor, sammenligner man altid mængden af den ønskede energiform man får ud, med den mængde energi man kommer ind: Når effektiviteten af motoren er 80% får man 80% af den elektriske energi, man putter ind, ud som bevægelsesenergi, mens 20% af energien bliver til spildvarme som ikke udnyttes.
Herunder kan du finde en kort gennemgang af de vigtigste energiformer. Du kan også læse mere i de enkelte artikler i leksikonet.
Kinetisk energi
Udgangspunktet er som sagt kinetisk energi der er den energi, et legeme har i kraft af sin bevægelse. Et legeme (fx en kugle) der bevæger sig med hastigheden v har en kinetisk energi som er halvdelen af produktet af legemets masse m og kvadratet på hastigheden: Ekin = ½ m·v2.
Man kan undre sig over faktoren ½ i definitionen. Så længe man kun har med kugler der støder ind i hinanden, at gøre, er den uden betydning. Thomas Young der indførte betegnelsen energi i 1807, definerede den faktisk som m·v2. Men hvis man gør det, kommer der til at stå 2-taller en masse andre steder i formlerne for fx potentiel energi, så derfor har det vist sig smartest at have ½ med her .
Hvis man beregner den kinetiske energi af en stålkugle i bevægelse hen over en glat overflade før den støder sammen med en anden kugle der ligger stille, og sammenligner med summen af de to kuglers kinetiske energier efter sammenstødet, er de to tal (næsten) ens. Det vil sige at den totale kinetiske energi af systemet bestående af de to kugler er (næsten) bevaret.
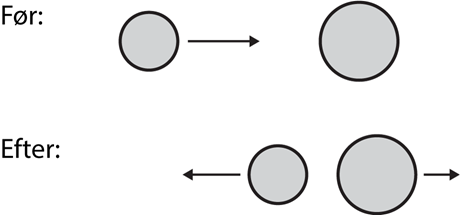
Grunden til at vi skrev 'næsten' ovenfor, er at det er en idealisering af den virkelige verden. I virkeligheden sker der under sammenstødet en lille deformation (sammentrykning) af kuglerne som bl.a. fører til at der udsendes lydbølger som bærer lidt af energien med sig; den samlede kinetiske energi er derfor en lille smule mindre efter sammenstødet. Hvis disse forhold kan ignoreres, kaldes sammenstødet 'elastisk'.
Potentiel energi
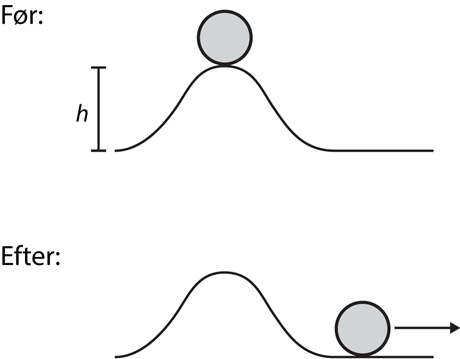
Lad os nu se på hvad der sker, når man kaster en bold, så den triller op ad en bakke. Jo højere op ad bakken den når, jo langsommere bevæger den sig. Hvor bliver den kinetiske energi af?
Den bliver omdannet til noget der kaldes potentiel energi. Det er den energi bolden har i kraft af sin beliggenhed i Jordens tyngdefelt. Man kan udregne den potentielle energi som m·g·h, hvor g = 9,8 m/s2 er tyngdeaccelerationen, boldens masse er m, og h er boldens højde over et eller andet referencepunkt.
Den samlede mekaniske energi af bolden, der er lig med summen af dens kinetiske og potentielle energi, ændrer sig ikke under dens bevægelse i tyngdefeltet, selv om den kinetiske og potentielle energi hver for sig ændrer sig. Det kan udtrykkes ved ligningen ½ m·v2 + m·g·h = konstant.
Denne ligning kan fx bruges til at beregne hvor hurtigt en bold vil bevæge sig, når den har rullet højden h ned ad en bakke: Den har så fået en hastighed v = √ g·h (hvis den lå stille til at begynde med).
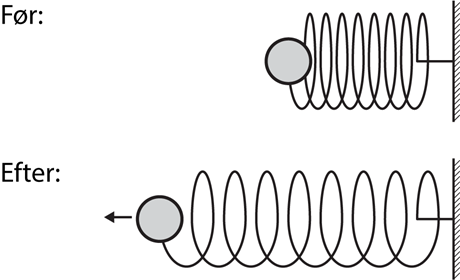
Det er ikke kun i forbindelse med tyngdefelter at man taler om potentiel energi. For eksempel har en ladet partikel i et elektrisk felt potentiel energi. Og en fjeder der er strakt eller trykket sammen, har potentiel energi.I eksemplet nedenfor vil bolden for enden af fjederen begynde med en høj potentiel energi der omdannes til kinetisk energi og tilbage til potentiel energi igen, i takt med fjederens svingning.
Mekanisk og indre energi
Summen af den kinetiske og den potentielle energi af bolden kalder man den mekaniske energi.
I de simple eksempler ovenfor er den mekaniske energi bevaret. Det er tilfældet så længe man kan se bort fra boldens indre struktur. Om man kan det, afhænger af boldens sammensætning og de kræfter der virker på den.
I virkeligheden består bolde og alle andre legemer jo af atomer som hver især kan bevæge sig. Hvis en stålkugle kastes ind mod en væg vil den komme tilbage med omtrent samme hastighed som den blev kastet med. Hvis kuglen derimod er lavet af modellervoks, vil den klaske ud mod væggen og ende med at ligge stille. Den mekaniske energi er åbenbart ikke bevaret i det tilfælde.
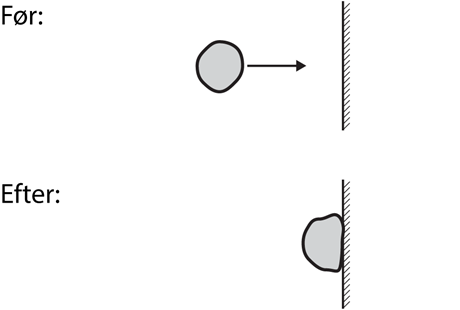
Hvad er der sket med den mekaniske energi? Den er blevet omdannet til indre energi i modellervoksen. For at forstå hvad der sker, må man skelne mellem makroskopisk bevægelse, dvs. bevægelsen af kuglen som helhed, og den individuelle bevægelse af de atomer der udgør kuglen. Atomerne er i konstant bevægelse på grund af den indre energi kuglen indeholder. Det er bl.a. kinetisk og potentiel energi af de atomer der udgør modellervoksen. Man kan forestille sig atomerne som små kugler forbundet med fjedre og i stadig tilfældig bevægelse frem og tilbage.
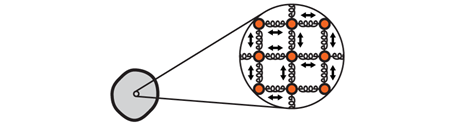
Udadtil manifesterer de atomare bevægelser sig som temperaturen af kuglen. Selv om den indre energi er mekanisk energi af atomerne, er den indre energi alligevel væsensforskellig fra den mekaniske energi, kuglen har i kraft af sin bevægelse som en helhed.
Når kuglen rammer væggen, vil modellervoksen ændre form hvorved små naboområder i dens indre gnider mod hinanden. Derved overføres der mekanisk energi til mindre og mindre længdeskalaer, og i sidste ende vil den mekaniske energi ende som mekanisk energi af de enkelte atomer.
På dette tidspunkt er den mekaniske energi blevet helt omdannet til indre energi. Når først det er sket, er den mekaniske energi i praksis gået tabt. Energien fra den ordnede bevægelse af kuglen er blevet fordelt på de mange, mange atomer som klumpen indeholder (i størrelsesordenen 1024, dvs. et 1-tal efterfulgt af 24 nuller), og sandsynligheden for at disses bevægelse ved et tilfælde skulle blive perfekt samordnede igen er så lille at det aldrig vil ske i Universets levetid.
Asymmetrien mellem makroskopisk og atomar bevægelse kan gøres præcis ved brug af begrebet entropi.
Andre energiformer
De fleste andre energiformer som elektrisk energi, kemisk energi og kerneenergi er i sidste ende potentiel energi eller en kombination af potentiel og kinetisk energi. For eksempel er kemisk energi den kinetiske og potentielle energi som elektronerne der udgør de kemiske bindinger, har.
Den eneste undtagelse er strålingsenergi, som er den energi som lys og anden elektromagnetisk stråling bærer. Denne energi er ikke knyttet til energien af materielle partikler, men findes i selve det elektromagnetiske felt.

